Distributive Property of Multiplication over Addition and Subtraction
Distributive property
Try it with numbers
Visual Representation
Visual Representation 2
Guided practice 1
Worksheet 1
Geometric Representation
Why do we need to know?
Distributing variables
Guided practice 2
Worksheet 2
Factoring
Guided practice 3
Worksheet 3
What is the Distributive Property?
The distributive property of multiplication over addition and subtraction is stated mathematically as
a·(b+c) = a·b+a·c. Here is a diagram that shows what we mean by
distribute.
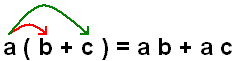
Notice that the a is distributed across the addition to b
and c. Take another look. See where the a,
b, and c start out and end up.
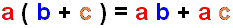
The distributive property also works with subtraction. a·(b-c) = a·b-a·c
Try it with Numbers
Let's check out the distributive property. We will use real numbers. Let a=2, b=3, and c=5. The equation can then be written 2·(3+5) = 2·3+2·5. We will take the left side of the equation first and simplify it.
| Result | Principle Used |
|---|---|
| 2·(3+5) | Left half of equation |
| 2·(8) | Simplify inside of the parenthesis first. 3+5=8, so we replace 3+5 with 8. |
| 2·8 | Since there is only one thing inside of the parenthesis, we can remove the parenthesis. |
| 16 | 2·8 = 16, so we replace 2·8 with 16. |
We just showed that the left half of the equation equals 16. Now we need to show that the right half of the equation is also 16.
| Result | Principle Used |
|---|---|
| 2·3+2·5 | Right half of equation |
| 6+2·5 | Since we do multiplication first, we will simplify 2·3. Since 2·3 = 6, we replace 2·3 with 6. |
| 6+10 | Now we multiply 2·5 = 10. So we replace 2·5 with 10. |
| 16 | Now we can add 6+10 = 16. |
So you can see that the distributive property of multiplication works.
Visual Representation of the Distributive property
Remember back to when you were learning how to multiply. Your teacher may have put a diagram like the following to represent 2·3:
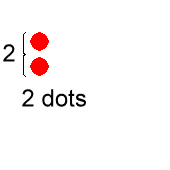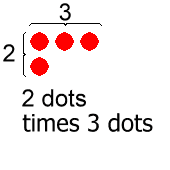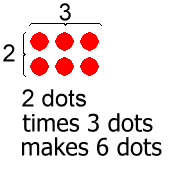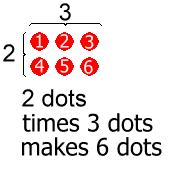
With 2 rows and 3 columns to represent 2·3, we can easily count the dots to conclude that 2·3 = 6.
Visual Representation of the Distributive property
Now let's use this representation of numbers with the distributive property. First we will represent 2·3+2·5, which is the right hand side of the equation.
Note that at the start, there are 2 rows of 3 dots (2·3) and 2 rows of 5 dots (2·5). You can see there are 16 dots. We mathemagically transform the dots to 2·(3+5) dots, which shows that 2(3 + 5) = 2·3 + 2·5 = 16.
Guided Practice 1
Write down each problem on a piece of paper. Simplify the expression using the distributive property. SHOW ALL OF YOUR WORK! DO NOT SIMPLIFY INSIDE THE PARENTHESIS FIRST! When you have an answer, click on the equation to see each step. Did you get each step right? If you got it right, move on to the next one. If you got it wrong, click on it to try it again.
Rule
a(b + c) = ab + ac
Process
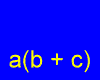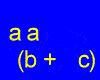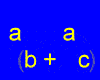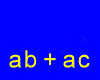
Example
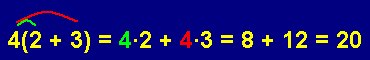
You try it
← Click on the expression to see the next step
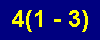
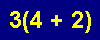
Worksheet 1
Click the "Make Worksheet" button to build a worksheet in a new window. Print the worksheet, do the problems on the worksheet, then check the answers at the bottom of the worksheet.
Geometric Representation of the Distributive property
|
|
|
Look at the diagram above. It uses lines with end points connected to represent addition. It uses rectangles to represent multiplication. Can you find the two lines together which make b + c? The length of the red line is b, and the length of the green line is c. When they are end to end, the length of the combined line is b + c. Now find the rectangle length a and width b. The area of a rectangle is length times width, which is written as l·w. In this case the length is a and the width is b. This means that the area of the rectangle is a·c. Next, find the rectangle which makes a·c. Since we are combining the area of the two rectangles, the total enclosed area is a·b + a·c. Now look at it another way. The top two lines have a length of b + c, and the line on the side has a length of a. So the area of the rectangle made up by these lines is a(b + c). This shows that a(b + c) = ab + ac, and ab + ac = a(b + c) |
Why do we need to know the distributive property?
The distributive property of multiplication is very important in solving algebraic equations. Look at the example of solving equations below. Notice that this example uses the distributive property. Don't worry if you don't yet understand how to solve these equations yet.
| Result | Principle Used |
|---|---|
| 3·(X - 4) = -3 | This is the equation to solve. |
| 3·X - 3·4 = -3 | Apply the distributive property. |
| 3·X - 12 = -3 | Multiply 3·4 to get 12. |
| 3·X - 12 + 12 = -3 + 12 | Add 12 to both sides. |
| 3·X = 9 | Combine like terms: -12 + 12 = 0 and -3 + 12 = 9 |
| (3·X)/3 = 9/3 | Divide both sides by 3. |
| (3/3)·X = 9/3 | Apply the commutative property of multiplication. |
| 1·X = 9/3 | Divide 3/3 to get 1. |
| X = 9/3 | Apply the property of multiplying by 1. |
| X = 3 | Divide 9 by 3. |
It is also important in factoring. When we have an expression that equals 0, we can factor to find the solutions. In these cases, we use the distributive property the other way around, which is ab+ac=a(b+c). Here is an example of factoring.
| Result | Principle Used |
|---|---|
| 3x-4x2=0 | This is the equation to factor. |
| 3x-4x·x=0 | An exponent means multiplication. |
| x(3-4x)=0 | Apply the distributive property. |
| x=0 or 3-4x=0 | Property of multiplying by zero. |
| x=0 or x=3/4 | Now simplify the expression |
Distributing Variables
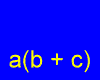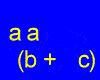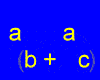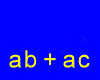
Since variables represent numbers, we can put a variable any place we find a number. Here are some examples:
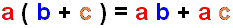
x·(3+2) = x·3+x·2
4·(a+2) = 4a+4·2
2·(3+t) = 2·3+2t
x·(y+z) = xy+xz
Guided Practice 2
Write down each problem on a piece of paper. Simplify the expression using the distributive property. SHOW ALL OF YOUR WORK! DO NOT SIMPLIFY INSIDE THE PARENTHESIS FIRST! When you have an answer, click on the equation to see each step. Did you get each step right? If you got it right, move on to the next one. If you got it wrong, click on it to try it again.
Rule
a(b + c) = ab + ac
Process
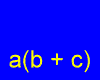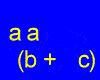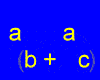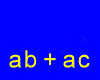
Example
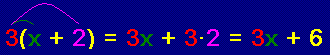
You try it
← Click on the expression to see the next step
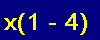
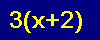
Worksheet 2
Click the "Make Worksheet" button to build a worksheet in a new window. Print the worksheet, do the problems on the worksheet, then check the answers at the bottom of the worksheet.
Factoring Using the Distributive Property
NOT IMPLEMENTED YET
Guided Practice 4
NOT IMPLEMENTED YET
Worksheet 4
Click the "Make Worksheet" button to build a worksheet in a new window. Print the worksheet, do the problems on the worksheet, then check the answers at the bottom of the worksheet.