Sets
Why do we need sets?
What is a set?
Members of a set.
Sets of numbers
Subsets
Why do we need sets?
In algebra, we understand the operations of addition (+) and multiplication (*). We can use these operations confident that the result will always be the same. For example, 1+2 always equals 3. We can depend on that fact whenever we do algebra. Also, according to the commutative law of addition, we can depend on the fact that 1+2 is always the same as 2+1.
For mathematicians, the question, "Why can we always depend on these results?" is very important. We can show graphically that 1+2 is the same as 2+1:
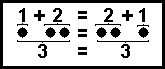
We could also show graphically that 1,242,392 + 47,392 is the same as 47,392 + 1,242,392, but that would take a lot of time and paper. Also, we would have to show it for every combination of values to be sure that the commutative law always holds true for any whole numbers.
This shows the need for generalized proofs of the principles of algebra. In order to prove this result for all number, mathematicians use the concept of sets. If we can prove a principle for one set (all whole numbers, for example), then for any other set that has the same characteristics (real numbers, for example), the proof will still hold.
What is a set?Let's start with the definition of a set.
In the definition, do you recognize the word collection? Do you collect anything? Some people collect stamps, or rocks. For our example we will use fruit.
Let's look at some examples that do not qualify as a set. Take the set of all tomatoes in Associated Food Warehouse #1234 that were picked on July 29 of the last year. These tomatoes are a collection of objects, but can membership be determined? If neither the boxes nor the tomatoes contain pick dates, it is impossible to determine which tomatoes belong to the groups. In this case, this does not constitute a set. Here is what may be another non-set: The collection of all rotten tomatoes in the warehouse. There are objects which form a collection, but can membership be established? What about two people who look at a particular tomato. One decided it is rotten, and the other decides that it is not rotten. Is it in the collection or not? In this case the collection is not a set because membership can not be established. On the other hand, if an objective criteria (a criteria that makes it so everyone can agree what is rotten or not) is established, then this collection does constitute a set.
|
Members of a Set
The definition of a set states that "membership can be established". When an object is
a member of a set, we say that it is an element of a set. Look at the diagram of set A.
Set A contains three objects, a, b, and
c. We say that a, b, and c
are elements
of set A. We can write a statement this way: A = { a, b, c }. This statement
says that the set A is composed
of exactly three elements, a, b, and c.
To state that a single object is an element of a set, we can write a ∈ A. This means that the object a is a member of the set A.
Notice that there are two objects which are outside the boundary of set A, the objects labeled d, and e. We say that d is not an element of A and write d ∉ A.
Sets of Numbers
In high school algebra, we usually deal with sets of numbers. Let's start with the set of integers. Let's use the definition of a set to see if integers really form a set. Do integers form a collection of objects about which membership can be established? The answer is, of course, yes. We can readily tell if a number is an integer or not. And, we know that anything that is not a number can not be an integer, and so is not a member of the set.
Another set of numbers is the set of real numbers. This is the set of all numbers. Since we can tell if an object is a number or not, membership can be easily established. The set of integers and real numbers can be subdivided into smaller sets. For example, the set of all positive numbers is set, since we can tell if an object is a positive number or not.
Subsets
| Definition 2: Set A is a subset of set B if and only if every member of set A is also a member of set B. |
If the set A is a subset of set B, we write A⊆B.