How Eratosthenes Calculated the Circumference of the Earth.
 |
Eratosthenes Calculating the Circumference of the Earth In the panel on the left, Eratosthenes is peering down a well in Syene to verify that the sun lights up the water at the bottom and that there are no shadows. In the second panel on the left, Eratosthenes is preparing to measure the length of the shadow of a pillar, so he can calculate the angle of the sun's rays. |
 Portrait of Eratosthenes |
Many attempts were made by ancient mathematicians to measure the circumference of the
earth. These mathematicians had mixed success. Eratosthenes attempt was, however, quite
successful, both from the point of view of accuracy and simplicity. Eratosthenes' estimate
was only 245 miles off the accurate value of 24,907, an error of less than 1%.
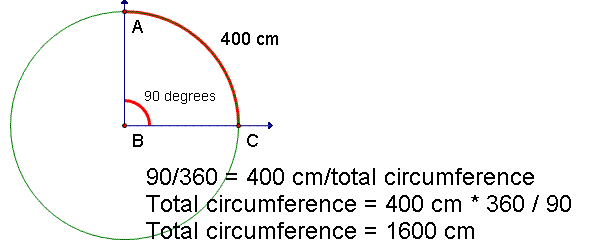
Eratosthenes estimate was based on proportions. The length of an arc of a circle is proportional to the measure of the angle of the rays from the center of the circle to the end points of the arc.
In the example to the left the measure of the angle containing the arc is 90 degrees. Since the measure of the angle of the entire circle is 360 degrees, the proportion of the measure of the arc angle to the measure of the angle of the whole circle is 90/360 = 1/4.
The measure of the arc is given as 400 cm. Since the ratio of the arc angle to the whole circle is 1/4, the ratio of the arc to the whole circle is the same. If we let C represent the circumference of the circle, 400 cm / C = 1/4. Multiplying both sides by 4 gives us 1600 cm / C = 1. Multiplying both sides by C gives us 1600 cm = C. We then know that the circumference of the circle is 1600 cm.
|
|
Eratosthenes Calculates the Circumference of the EarthEratosthenes knew from travelers that during the summer solstice, an upright stick cast no shadow. This Eratosthenes knew this meant the sun was directly overhead. To verify this, he traveled to Syene for the summer solstice and peered down a well. He was able to see that the water at the bottom of the well was lit by the sun, and that the walls of the well cast no shadow on the water. Eratosthenes also knew that the distance from Syene to Alexandria had been measured as 5000 stadia. He also believed that the two cities were on the same meridian (directly north or south of each other). These conditions were perfect to calculate the circumference of the earth. On another summer solstice, Eratosthenes traveled to Alexandria. There he observed the shadow of a pillar and measured the sun's angle from the zenith (directly overhead) as 7 degrees 12 minutes, or 1/50 of the measure of the angle of a circle. This gave the circumference a measure of 250,000 stadia. For reasons we do not know, Eratosthenes added 2000 stadia to this measure to account for error, giving a final measure of 252,000 stadia. |
PDF Version
Download a one page PDF version of this document.