Nicole Oresme's Proof That the Harmonic Series Diverges
The Harmonic Series
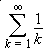is called the harmonic series. In general, a harmonic
series is any series that can be expressed in the form 
.
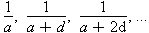Whether or not a series
diverges (grows towards infinity), or converges (grows towards a finite number) was argued
for many years. Notice that when we write out the first few terms of the harmonic series that each
term is getting smaller and smaller: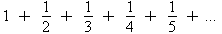 
. This tells us this series might converge,
but does not guarantee that it converges.
The French mathematician Nicole Oresme (ca. 1323-1382) was the first to demonstrate that the harmonic
series diverges. Her method is simple and elegant. It is easy to conclude that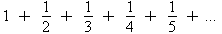
>= 
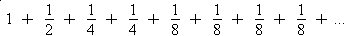. Regrouping this series we get: 
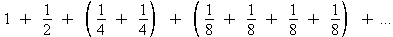. This can easily be rewritten as: 
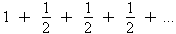. Since the series 1 + 1/2 + 1/2 + 1/2 + ... does not converge, then the harmonic
series can not converge either. As you see, this demonstration has the disadvantage of requiring a
proof that a finite series of sequential terms of the harmonic series can always be found that
sums to more than 1/2.
Citation
Cite this source as:
McAdams, David E., "Nicole Oresme's Proof That the Harmonic Series Diverges", from LifeIsAStoryProblem.org, 30 June 2007, URL https://lifeisastoryproblem.tripod.com/numbers/oresmeharmonicseries.html
Other Resources
Harmonic Series Eric W. Weisstein, From MathWorld--A Wolfram Web Resource.