Direct Instruction Model
- From National Council of Teachers of Mathematics
- Problem Solving Standards: Instructional programs from pre-kindergarten through grade 12 should enable all students to:
- apply and adapt a variety of appropriate strategies to solve problems.
- Reasoning and Proof Standard: Instructional programs from pre-kindergarten through grade 12 should enable all students to:
- select and use various types of reasoning and methods of proof.
- Communication Standard: Instructional programs from pre-kindergarten through grade 12 should enable all students to:
- organize and consolidate their mathematical thinking through communication;
- communicate their mathematical thinking coherently and clearly to peers, teachers, and others.
- Representation Standard: Instructional programs from pre-kindergarten through grade 12 should enable all students to:
- create and use representations to organize, record, and communicate mathematical ideas;
- select, apply, and translate among mathematical representations to solve problems;
- use representations to model and interpret physical, social, and mathematical phenomena.
- Problem Solving Standards: Instructional programs from pre-kindergarten through grade 12 should enable all students to:
- From Utah Educator Network Core Curriculum:
- Standard 3 - Students will solve problems using spatial and logical reasoning, applications of geometric principles, and modeling.
- Objective 3 - Solve problems using visualization, spatial reasoning, and geometric modeling.
- Standard 3 - Students will solve problems using spatial and logical reasoning, applications of geometric principles, and modeling.
At the end of the lesson the student will be able to:
- Represent basic one and two dimensional mathematics operations with geometric figures.
- Identify strengths and weaknesses of geometric figures.
- Weaknesses
- Arrays of dots are mainly useful for representing integers.
- Any geometric representation is inexact. Try drawing a line with a length of exactly π.
- Strengths
- The visualization of an algebraic relationship can help in understanding the relationship.
- Weaknesses
- Identify parts of a graph in Cartesian Coordinates.
- Show an emerging ability to represent three dimensional mathematics operation by building and explaining a three dimensional model of (a + b)3.
- This lesson requires the use of a straight edge and drawing surface for the teacher. This can be a white board, an overhead transparency, or other.
- Each student will need a straight edge and a drawing surface such as paper or personal whiteboard to draw figures.
- Each student will need a visualization worksheet.
- The teacher can use an overhead transparency of the visualization worksheet while guiding students through the process.
Direct Instruction Model
- Gathering Activity - Think, Pair, Share.
Have the students write in their journals how they might represent the equation 3 + 5 = 8 using a drawing. After a few minutes, have the students pair up and compare their representations. Have them discuss the relative merits of the various representations. Have each pair share with the class their representation and its merits. - Internet Activity (optional)
Explore representations using Introduction to Geometric Representation in Algebra. This activity can be used in conjunction with the worksheet. - Review - Measurement
Activate prior knowledge of measurement of lengths by discussing various ways
to measure the length of a line. Then ask the class to identify the area of a
3 x 5 rectangle. Ask if this is a reasonable representation
of the algebraic fact 3 · 5 = 15.
- State the problem and objective
- State that geometric representations of algebraic principles can help us understand.
- State and write on the board that the student will be able to:
- Represent addition and multiplication with arrays of dots and with lines.
- Identify strengths and weaknesses of geometric figures.
- Identify parts of a graph in Cartesian Coordinates.
- Show an emerging ability to represent three dimensional mathematics operation by building and explaining a three dimensional model of (a + b)3.
- Guided Practice - Visualization Worksheet
- Introduce the idea of three dimensional models of algebraic relationships.
- Refer to the one dimensional model of a + b and the two dimensional model of (a + b)2 = a2 + 2ab + b2 in the worksheet.
- Ask the students how they might represent (a + b)3 = a3 + 3a2b + 3ab2 + b3.
- Pass out the template for (a + b)3. Have the students assemble the three dimensional figure, and then explain it to their partner. When they are ready, have them explain it to the teacher.
- Blind students will need accommodations to understand, interpret, and draw geometric figures.
- Students with cognitive difficulties will need additional assistance bridging from the concrete figure to the abstract algebraic meaning.
- Students with difficulty in fine motor skills may need assistance assembling their model of (a + b)3
- Some students may want to orally describe lines and points rather than in writing.
- An informal assessment for learning will be performed by listening to students' contributions to discussion.
- An informal assessment for learning will be performed by reviewing the students' notes.
- A formal assessment for learning will be performed by grading the students' worksheets.
- A formal assessment of learning will be performed by listening to the students' explanations of the model representing (a + b)3.
- Math Line Art
Thumbnail Link Description 
Circle 1 Line Art Do-it-yourself circle line art page to print and draw. 
Circle 2 Line Art Do-it-yourself circle line art page to print and draw. 
Triangle 22 Line Art Do-it-yourself triangle line art page to print and draw. 
Pentagon 17 Line Art Do-it-yourself pentagon line art page to print and draw. 
Square 22 Line Art Do-it-yourself square line art page to print and draw. 
Line Intersection 1 Line Art Do-it-yourself line intersection line art page to print and draw. - Geometric Nets
Example Name Description Printable Net 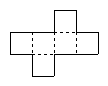
Cube
A cube is a regular polyhedron made up of squares
net_cube.pdf 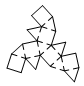
Cuboctahedron
Cuboctahedron
net_cuboctahedron.pdf 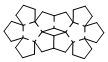
Dodecahedron
Dodecahedron
net_dodecahedron.pdf 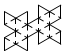
Icosahedron
Icosahedron
net_icosahedron.pdf 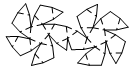
Icosidodecahedron
Icosidodecahedron
net_icosidodecahedron.pdf 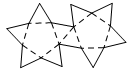
Pentagonal antiprism
A pentagonal antiprism is a 12 sided solid consisting of two pentagons connected by alternating triangles.
net_pentagonal_antiprism.pdf 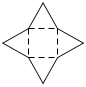
Rectangular pyramid
A rectangular pyramid has a square base and triangles coming to a point. In this example, isosceles triangles are used.
net_rectangular_pyramid.pdf 
Snub cube
A snub cube
net_snub_cube.pdf 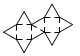
Square antiprism
A square antiprism consists of two squares connected by alternating triangles.
net_square_antiprism.pdf 
Tetrahedron
A tetrahedron
net_tetrahedron.pdf 
Dodecahedron
A dodecahedron
net_trunc_dodecahedron.pdf 
Truncated cube
A truncated cube is a cube whose corners have been truncated, or 'cut off'. Each side of the cube becomes a regular octahedron (an eight sided figure where the length of each side is the same), and the corners become isosceles triangles.
net_truncated_cube.pdf
Download Template for (a + b)3 = a3 + 3a2b + 3ab2 + b3
Download Visualization Worksheet.