Unit Plan - Introduction and Review for Intermediate Algebra

Notes:

This unit starts with a get-to-know-you activity. It continues with a learning activities intended to stretch student visualization abilities, and to set the tone for the class.

The unit continues with a review of the basic principles and tools of Intermediate Algebra, including:

  • Elementary Number Theory including:
    • Properties of numbers
      • Integers, rational numbers, irrational numbers and real numbers
      • Magnitude of numbers and absolute value
      • Addition: closure, identity, inverse, commutativity, associativity
      • Multiplication: closure, identity, inverse, commutativity, associativity
      • Distributive property of multiplication over addition
      • Properties of exponents
    • Basic operations on numbers including exponents and square root
    • Order of operations
  • Variables and variable expressions
    • Variables
    • Evaluating variable expressions
    • Multiplying variable expressions (including distributive property of multiplication)
    • Factoring variable expressions
    • Operations on rational expressions
  • Solving linear equations
  • Ratios
  • Identities and false statements
  • Solving linear inequalities
  • Statistics including mean, median and mode
  • Dimensional analysis
  • Graphing points and functions, transformations
  • Math logic

This document can be found on the Web at http://www.lifeisastoryproblem.net/lesson/UPMLIntroAlgebra.html.

Stage 1 - Desired Results

Established Goals: What is this?

Note: "Core of the Core" goals are denoted with the symbol ‡.

From National Council of Teachers of Mathematics

Number and Operations Standard

Understanding numbers, ways of representing numbers, relationships among numbers, and number systems

Instructional programs should enable all students to:

  • ‡work flexibly with fractions, decimals, and percents to solve problems;
  • compare and order fractions, decimals, and percents efficiently and find their approximate locations on a number line;
  • use factors, multiples, prime factorization, and relatively prime numbers to solve problems;
  • develop meaning for integers and represent and compare quantities with them;
  • develop a deeper understanding of very large and very small numbers and of various representations of them;
  • compare and contrast the properties of numbers and number systems, including the rational and real numbers;
  • use number-theory arguments to justify relationships involving whole numbers.

Understanding meanings of operations and how they relate to one another

Instructional programs should enable all students to:

  • ‡understand the meaning and effects of arithmetic operations with fractions, decimals, and integers;
  • ‡use the associative and commutative properties of addition and multiplication and the distributive property of multiplication over addition to simplify computations with integers, fractions, and decimals;
  • ‡understand and use the inverse relationships of addition and subtraction, multiplication and division, and squaring and finding square roots to simplify computations and solve problems.
  • judge the effects of such operations as multiplication, division, and computing powers and roots on the magnitudes of quantities;

Computing fluently and make reasonable estimates

Instructional programs should enable all students to:

  • ‡select appropriate methods and tools for computing with fractions and decimals from among mental computation, estimation, calculators or computers, and paper and pencil, depending on the situation, and apply the selected methods;
  • develop and analyze algorithms for computing with fractions, decimals, and integers and develop fluency in their use;
  • develop and use strategies to estimate the results of rational-number computations and judge the reasonableness of the results;
  • develop, analyze, and explain methods for solving problems involving proportions, such as scaling and finding equivalent ratios.
  • develop fluency in operations with real numbers, vectors, and matrices, using mental computation or paper-and-pencil calculations for simple cases and technology for more-complicated cases.
  • ‡judge the reasonableness of numerical computations and their results.

Algebra

Understanding patterns, relations, and functions

Instructional programs should enable all students to:

  • ‡represent, analyze, and generalize a variety of patterns with tables, graphs, words, and, when possible, symbolic rules

Representing and analyzing mathematical situations and structures using algebraic symbols

Instructional programs should enable all students to:

  • ‡develop an initial conceptual understanding of different uses of variables;
  • explore relationships between symbolic expressions and graphs of lines, paying particular attention to the meaning of intercept and slope;
  • ‡use symbolic algebra to represent situations and to solve problems, especially those that involve linear relationships;
  • recognize and generate equivalent forms for simple algebraic expressions and solve linear equations;
  • understand the meaning of equivalent forms of expressions, equations, inequalities, and relations.

Using mathematical models to represent and understand quantitative relationships

Instructional programs should enable all students to:

  • ‡model and solve contextualized problems using various representations, such as graphs, tables, and equations.

Analyzing change in various contexts

Instructional programs should enable all students to:

  • use graphs to analyze the nature of changes in quantities in linear relationships.

From Utah Educator Network:

Elementary Algebra Content

  • 1.1 - ‡Compute fluently and make reasonable estimates.
  • 1.2 - ‡Represent real numbers in a variety of ways.
  • 1.3 - Identify relationships among real numbers and operations involving these numbers.
  • 2.1 - ‡Use patterns, relations, and functions to represent mathematical situations.
  • 2.2 - ‡Evaluate, solve, and analyze mathematical situations using algebraic properties and symbols.
  • 2.3 - Represent quantitative relationships using mathematical models and symbols.
  • 3.3.3 - Illustrate multiplication of polynomials using area models, e.g., (a + b)2, x(x + 2), or (x + a)(x + b).

Intermediate Algebra Content

  • 1.1.1 - ‡Simplify numerical expressions with rational exponents.
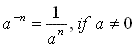  • 2.2.9 - ‡Recognize that a-n is defined as the reciprocal of an, i.e., a^(-n) = 1/(a^n) if a<>0.
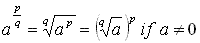  • 2.2.10 - ‡Recognize that rational exponents are used to represent radicals, i.e., a^(p/q)=q root of (a^p)=(q root of a)^p if a<>0.
  • 3.3.1 - Solve problems involving absolute value and quadratic functions algebraically and graphically.
Understandings: What is this?
  • Life is a story problem.
  • Numbers and variables representing numbers can be manipulated according to certain rules.
  • Mathematical definitions of common words can be different from the definitions we know from daily life.
  • Real-life problems can be solved using equations with variables.
Essential Questions: What is this?
  • "Why do I need to learn algebra?"
  • "How am I going to use this stuff?"
  • "What if I'm not good at math?"
  • "How can I understand all the math words?"
Students will know/be able to: What is this?
  • Students will reacquire skills in manipulating and interpreting numbers.
  • Students will be able to identify ways in which math shows up in daily life.
  • Students will reacquire skills in manipulating expressions with variables and solving linear equations and inequalities.
  • Students will be able to express mathematical principles with pictures or diagrams, algebraic symbols, and with words.
Stage 2 - Assessment Evidence
Performance Tasks:
  • Students will identify ways in which math shows up in daily life.
  • Students will write clear definitions of math terms.
  • Students will demonstrate the ability to simplify algebraic expressions and solve simple algebraic equations.
  • Students will demonstrate the ability to manipulate the different forms of exponents and radicals.
  • Students will demonstrate the ability to identify numbers as integers, rational numbers, irrational numbers, and real numbers.
Other Evidence
  • Students will participate in class presentations.
  • Students will respond to questions in class.
  • Students will ask questions in class.
  • Students will complete pre and post learning assessment instruments.
Stage 3 - Learning Plan
Unit Structure:
This unit is intended to be mainly taught in small groups, with the single exception of the first two lessons, Life is a Story Problem, and Visualizing in Mathematics. Some of the students will need more instruction than others, so enrichment activities are included. Each lesson starts with a quick review and a pretest. Students who score 80% or above on the pretest move to the next lesson immediately. Other students will be presented a lesson with a packet intended to provide sufficient scaffolding for most students.
Learning Activities:

Activity
Type

Lesson
Model

Description
Motivate Motivational Model Life is a Story Problem

This lesson is intended to frame the course, its requirements, and motivate the students to study math. It answers such questions as, "Why is this class required anyway?", "Will there be a lot of homework?", and "What do I have to do to get an 'A'?"

Equip
Revise		 Direct Instruction Model Visualizing in Mathematics

This lesson reintroduces the various methods of visualizing in mathematics. It introduces the student to 3-D visualizations.

View lesson plan: html | PDF

Equip
Revise		 Concept Development Model Adding and Subtracting Positive and Negative Numbers

This lesson reviews adding and subtracting positive and negative numbers.

View lesson plan: html | PDF

Equip
Revise		 Link Memorization Model Properties of Real Numbers

This lesson reviews the properties of real numbers, including associative, commutative, distributive, and absolute value.

View lesson plan: html |

Other Resources

Rational Numbers and Proportions from NCTM Illuminations.

ATHERTON J S (2005) Learning and Teaching: Motivation [On-line] UK: Available: http://www.learningandteaching.info/learning/motivation.htm Accessed: 3 November 2006

ATHERTON J S (2005) Learning and Teaching: Motivational Hygiene [On-line] UK: Available: http://www.learningandteaching.info/learning/motivation.htm Accessed: 3 November 2006

ATHERTON J S (2005) Learning and Teaching: Motivation and Anxiety [On-line] UK: Available: http://www.learningandteaching.info/learning/motivanx.htm Accessed: 3 November 2006

Understanding Rational Numbers and Proportions, by Frances R. Curcio and Nadine S. Bezuk, as found in the Addenda Series, NCTM, (1992), pp. 13-18, 24-27.